
மெர்சென் எண்
இதை குறிக்க M பயன்படுகிறது. மெர்சென் எண் என்பது இரண்டின் அடுக்கு எண் கழித்தல் ஒன்று என்னும் வடிவில் எழுதத்தக்க ஒரு நேர்ம முழு எண்.. or
or 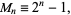
மேற்கண்டவாறு எழுதத்தக்க மெர்சென் எண் பகா எண்ணாக இருந்தால் அதனை மெர்சென் பகாத்தனி - Mersenne prime என்று வரையறை செய்வர்.
பகா எண் என்றால் ஒன்றாலும் தன்னாலும் மட்டும் வகுபடும் எண்கள் எனப்படும் என சின்ன வகுப்பில் கற்று இருப்பீர்கள்.
இவ் எண்கள் பற்றி தமிழில் விக்கிபீடியா தெளிவாக குறிப்பிடுகிறது. ஆனால் ஆங்கிலத்திலே தான் பூரண புதிய தகவல்கள் தொகுக்கப்பட்டு உள்ளது
முன்னனி Mersenne primeஎண்கள் :
| # | digits | year | discoverer (reference) | value | |
| 1 | 2 | 1 | antiquity | 3 | |
| 2 | 3 | 1 | antiquity | 7 | |
| 3 | 5 | 2 | antiquity | 31 | |
| 4 | 7 | 3 | antiquity | 127 | |
| 5 | 13 | 4 | 1461 | Reguis (1536), Cataldi (1603) | 8191 |
| 6 | 17 | 6 | 1588 | Cataldi (1603) | 131071 |
| 7 | 19 | 6 | 1588 | Cataldi (1603) | 524287 |
| 8 | 31 | 10 | 1750 | Euler (1772) | 2147483647 |
| 9 | 61 | 19 | 1883 | Pervouchine (1883), Seelhoff (1886) | 2305843009213693951 |
| 10 | 89 | 27 | 1911 | Powers (1911) | 618970019642690137449562111 |
| 11 | 107 | 33 | 1913 | Powers (1914) | 162259276829213363391578010288127 |
| 12 | 127 | 39 | 1876 | Lucas (1876) | 170141183460469231731687303715884105727 |
| 13 | 521 | 157 | Jan. 30, 1952 | Robinson (1954) | 68647976601306097149...12574028291115057151 |
இதன் இறுதியாக கண்டுபிடிக்கப்பட்ட இலக்கம் 48 வது எண் ஆகும். இது இணையத்தில் உள்ள GIMPS எனப்படும் Great Internet Mersenne Prime Search ஆல் இவ்வருடத்தின் மாசி மாதத்தின் முதலாவது வாரத்தில் கண்டு பிடிக்கப்பட்டது. இதற்காக விசேடமான மென்பொருள் ஒன்று தன்னார்வ தொண்டர்களின் கணனியில் நிறுவப்பட்டு 360,000 processors ஒரு செக்கனுக்கு 150 trillion செய்கைகள் இணையம் மூலம் ஒன்றிணைக்கப்பட்டு கண்டறியப்பட்டது.
இது முதலாவது Mersenne Number பற்றிய விளங்கப்படுதப்பட்டு 350 வருடங்களின் பின்னர் கண்டறியப்பட்ட 48 வது Mersenne Number ஆகும்.
48 வது mersenne எண் என்னவென்று இன்னமும் சொல்லவே இல்லை என்று நினைக்கலாம். அதை சொல்ல முடியாது. ஏன் என்றால் அது 17,425,170 இலக்கத்தில் உள்ளது. அதாவது 257,885,161 − 1 எண் ஆகும்.
மெர்சென் எண்களின் பயன்பாடு
இவை பெரும்பாலும் கணணி துறையில் தகவல்களை இரகசிய படுத்த பயன்படுத்த படுகிறது.
கணனியில் விளையாட்டுக்களில் மெய்நிகர் தன்மையை தீர்மானிப்பதிலும் இவையே பயன்படுகிறது. இதன் அடிப்படையில் தான் மக்கள் பயன்படுத்தும் தானியங்கி பணம்வழங்கி முதல், நாளொன்றுக்குப் பல பில்லியன் dollars கணக்கில் பண மாறாட்டம் நடைபெறும் பங்குச் சந்தைக் கொடுக்கல்-வாங்கல்கள் நடைபெறுகின்றன.
அத்துடன் ஒழுங்குபடுத்தும் algorithm களிலும் அதிகளவில் பயன்படுகிறது. எவ்வாறாயினும் பிபனோச்சி எண்கள் அளவிற்கு இல்லை.
முடிவு
மெர்சென் எண்கள் என்பது Number theory ல் சிக்கலான ஒன்று. இதுவரை தீர்க்கப்படாத சந்தேகங்களில் ஒன்று. பல இடங்களில் பயன்படும் ஒன்று.
அண்மையில் MATLAB 2013a இல் இயங்கும் சந்தர்ப்பம் கிடைத்த போது தான் இதை பற்றி கொஞ்சம் அறிந்தேன் . அறிந்ததை உங்களுடன் பகிர்கிறேன்.