கணிதத்தில் சதுர எண்கள், முக்கோண எண்கள். வர்க்க மூல எண்கள், சிக்கல் எண்கள் என பலவகையனவை உண்டு. அதில் ஒன்று தான் இந்த Fibonacci எண்கள். இதை பற்றி தமிழில் விக்கி மற்றும் இன்னொரு தளத்தில் மட்டுமே அறிமுகங்கள் உள்ளன. பிபனோச்சி தினம் 05.08.13 (mm/dd/yyyy) என்ற திகதி ஒழுங்கில் வந்ததால் நேற்று பல நாடுகளில் கொண்டாடப்பட்டது. என்றாலும் 05.08.13 (dd/mm/yyyy) என்ற நாம் பயன்படுத்தும் திகதி இடல் முறையை பார்த்தால் எமக்கு இனி தான் இந்த தினம் வரும். அடுத்த இத்தினம் Aug 13, 2021 இல் வரும்.. இந்த பிபனோச்சி எண்கள் பற்றி ஒரு தொகுப்பாக இந்த பதிவு அமைகிறது.கட்டுரைக்கு முதல், நான் இதை பற்றி பெரிதாக அறிந்திருக்க வில்லை. இணையத்தில் கிடைக்கும் தகவல்களை தொகுத்து இலகு படுத்தி உள்ளேன். அவ்வளவு தான். உங்கள் விமர்சனங்களை தெரிவிக்கலாம்.
‘Simple'ளா கேக்கிறேன், 24157817 Fibonacci number'ரா?
ஆமா, 22வது Fibonacci number ... By the way ... அது மந்தைவெளி P.சுப்ரமணியத்தோட Phone Number"
இந்த வசனமே முதன் முதலில் தமிழர்கள் இடையே Fibonacci number பற்றிய எண்ணத்தை அறிமுக படுத்தியது.
‘எந்திரன்’ படத்தில் வந்த வசனமே இது. படத்தை பார்த்தீர்களே தவிர இதை பற்றி சிந்தித்தீர்களா? (நான் படம் பார்க்கவே இல்லை).உலகின் அடிப்படையே இந்த எண்கள் தான் என்கிறார்கள் விஞ்ஞானிகள்.
பிபனோச்சி எண்கள்
13ம் நூற்றாண்டில் இத்தாலியக் கணித மேதை Leonardo of Pisa ( Leonardo Fibonacci என்றும் பெயர் உண்டு) என்பவர் வகுத்த எண் வரிசைதான் இந்த Fibonacci number.
0 இல் தொடங்கி, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 என்று செல்கிறது இந்த எண் வரிசை. இந்த வரிசையை உற்று கவனித்தாலே தெரிந்துவிடும். ஒரு எண் தனக்கு முன் உள்ள எண்ணோடு கூட்டப்பட்டு அந்தக் கூட்டுத் தொகையே அடுத்த எண்ணாக இந்த வரிசையில் அமர்கிறது.
சுருங்க சொன்னால் :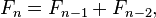 
[இங்கு: 
]
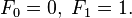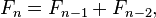[இங்கு: 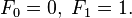]விளக்கமாக சொன்னால்
இவ் எண்தொடரும் இதன் பண்புகளும் கணக்கில் அதிகம் தொடர்பு இல்லாதவரையும் ஈர்க்கும் ஒரு கணிதக் கருத்து. இது இயற்கையில் அதிகளவு காணப்படுகிறது. அதை விட ஆதிகால மனிதர்களின் படைப்புகளிலும் நிறையவே உண்டு.
ஃபிபனாச்சி மரம், தொடரும் பின்னம், ஒருங்குகள் ஒருங்கும் வேகம், பாஸ்கல் முக்கோணம் பற்றி அடிப்படைகள் தமிழ் விக்கிபீடியாவில் தொகுத்துள்ளனர். (உசாத்துணையில் காண்க)
Golden Number
இதற்கு ஆழமான விளக்கங்கள் உண்டு. சுருங்க சொன்னால் ஒரு F எண்ணை அதற்கு முதல் உள்ள f என்னால் பிரிக்கும் போது வரும் விடை. இது எப்போதும்
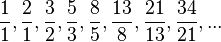= 1.618 ... இல் அமையும்Fibonacci numbers அவதானிக்கப்படும் இடங்கள்
மனித உடலில்
முதலில் எம் உடலில் இவை எங்குள்ளன என்று பார்ப்போம்.. "எங்கு என்றால்? இந்த எண் தொடரில் அமைந்த சில பாகங்கள் பற்றி காண்போம்.1. இது உங்கள் கை விரலில் உள்ள எலும்புகளின் நீளத்தில் உள்ளது.
நீங்களே செய்து பார்க்க முதலில் மௌஸ் மீது இருந்து கையை எடுத்து அதில் சுட்டு விரலை கீழே உள்ள படத்தில் பொருந்துமாறு வைத்து பாருங்கள். உங்கள் எலும்புகளின் நீளங்கள் Fibonacci ratio ஆகிய 1.618 இல் அமைந்து இருப்பதோடு Fibonacci numbers இல் 2, 3, 5 , 8 உடன் பொருந்துகின்றன.
2. மனித கையில் முன் பகுதியின் விகிதம் 1.618 இல் இருக்கும்
3. பாதங்களில் பிரிப்பு விகிதம் கூட Golden Number இல் இருக்கும்.
இதன் ஆச்சரியமே நீங்கள் குள்ளமானவராக, நெட்டையனவராக எப்படி இருந்தாலும் Golden number விகிதத்திலே தான் உங்கள் மேல் சொன்ன பாக நீளங்கள் இருக்கும்.
இன்னும் சொல்லலாம்:
- மூக்கு -1 துளை 2
- ஒரு உடல் - 2 கைகள் - ஒரு கையில் 5 விரல்
- இனப்பெருக்க தொகுதி
விலங்குகளில்
- வண்ணத்து பூசியில் உடல் கோலங்கள்
- முயல்களின் இனப்பெருக்கம்
- Nautiluses உயிரின ஓட்டின் பிரிப்பு
- பசுக்கள் இனம் பெருகும் விகிதம்
- தேனீ கூட்டில் உள்ள தேனிகள் எண்ணிக்கை
தாவரங்களில்
- உங்கள் வீட்டு தோட்டத்தில் உள்ள மரத்தின் கிளைகள்
- அன்னாசியில் உள்ள முகிழ்களின் எண்ணிக்கை
- சூரியகாந்தி பூவின் இதழ்களின் எண்ணிக்கை - பொதுவாக அனைத்து பூக்களுமே இதே எண் தொடரில் தான் இருக்கும்.
- வாழைப்பழத்தை குறுக்கே வெட்டினால் 3 பிரிவுகள், அப்பிள் பழத்தில் 5 பிரிவுகள்
கட்ட கலையில்
- காஸா பிரமிட்களில் உயர விகிதம் (Base:height:slant height)
- பிரான்சில் உள்ள Chartres Cathedral
- இந்தியாவின் தாஜ் மகால்
- ஏதெனஸில் உள்ள Parthenon
- மோனாலிசா ஓவிய முக அமைப்பு
மேலும் சில:
- குதிரை பந்தயத்தில் ஜெயிக்கும் குதிரைகைளின் எண்களின் வரிசை இதில் இருக்குமாம்.
- விண்வெளியில் உள்ள நட்சத்திரக் கூட்டங்களில் உள்ள நட்சத்திர எண்ணிக்கை
- பங்குச் சந்தையின் ஏற்ற இறக்கங்கள் இவ் வரிசையின் அடிப்படையில் நடைபெறுகிறதாம்
- உலக இலக்கியங்கள் அனைத்திலும் உள்ள யாப்பு அமைப்பு முறை கூட இந்த எண் வரிசையை அடிப்படையாக கொண்டவை
நீங்களும் பிபனோச்சி எண்களும்
நீங்கள் கூட இவ்வாறு இந்த எண் தொடரில் அமைந்த இயற்கையை காண முடியும். நிச்சயம் ஒருநாள் நீங்கள் சந்திக்கும் ஏதோ ஒரு நிகழ்வு - இயற்கையால் ஆளப்படும் இடத்தில் இந்த எண் வரிசையை உணர்வீர்கள். உங்கள் வாழ்க்கையில் சில தருணங்களில் முடிவு எடுக்கும் போது இந்த தொடரையும் கவனத்தில் கொள்ளுங்கள். உங்களுக்கு சாதகமான / எதிர் பார்க்கும் முடிவுகள் கிடைக்கலாம்!!
உசாத்துணை :
- Fibonacci number - En Wiki Pedia
- Fibonacci number - தமிழ் விக்கி
- Fibonacci Number - Wolfram
- maths.surrey.ac.uk//Fibonacci
- இயற்கையில் சில ஒழுங்குகள் - environmentalgraffiti
- Pintrest இல் ஒரு பிரமாண்ட பட தொகுப்பையே காணலாம் - pinterest.com
இதன் மற்ற பகுதிகளை பற்றி இன்னொரு பதிவில் காணுங்கள்...